The concept of the rank of a matrix is a fundamental topic in linear algebra that plays a crucial role in various applications, from engineering to data science. In this article, we’ll explore the definition of matrix rank, its calculation methods, significance, and real-world applications. Buckle up as we dive deep into the world of matrices!
What is the Rank of a Matrix?
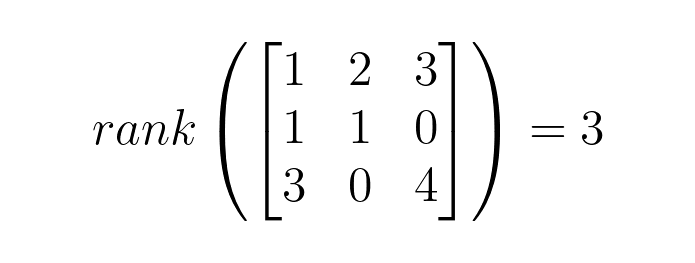
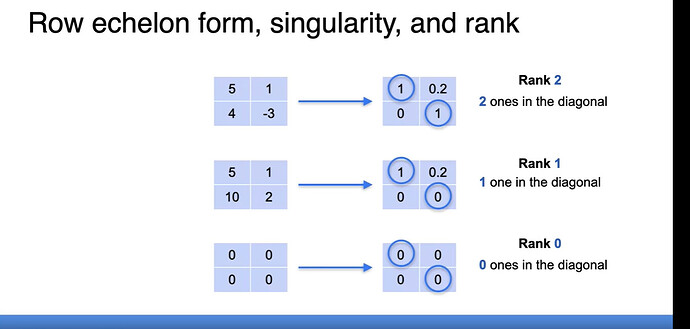
The rank of a matrix is a measure of the dimensionality of the vector space generated by its rows or columns. Essentially, it tells us how many of its rows or columns are linearly independent. A matrix can have several properties based on its rank, making it an essential concept in both theoretical and applied mathematics.
To grasp the rank of a matrix, we need to understand linear independence. A set of vectors is said to be linearly independent if no vector can be expressed as a linear combination of the others. Conversely, if at least one vector can be expressed this way, the set is linearly dependent.
Mathematically, the rank of a matrix AAA is defined as the maximum number of linearly independent column vectors in the matrix. This can also be applied to the row vectors; hence, the rank of a matrix can be determined from either the rows or the columns, and it will yield the same value.
Key Characteristics of Matrix Rank
- Rank and Dimensions: The rank gives us insights into the dimensions of the image and kernel of a linear transformation associated with the matrix. If the matrix is m×nm \times nm×n, its rank cannot exceed the smaller of mmm and nnn.
- Full Rank: A matrix is said to be of full rank if its rank equals the smallest of its dimensions. For an m×nm \times nm×n matrix, if rank = min(m,n) \min(m, n)min(m,n), the matrix is full rank. This implies that all rows or columns are linearly independent.
- Zero Rank: A matrix with no non-zero rows or columns has a rank of zero. This indicates that the matrix does not span any dimension in its corresponding vector space.
How to Calculate the Rank of a Matrix
Calculating the rank of a matrix can be done through several methods. The most common approaches include the Row Echelon Form (REF), Reduced Row Echelon Form (RREF), and using determinants. Let’s delve into these methods step-by-step.
- Row Echelon Form (REF)
The first method to calculate the rank of a matrix is converting it to Row Echelon Form. This involves a series of row operations aimed at simplifying the matrix. The steps typically include:
- Swapping rows.
- Multiplying a row by a non-zero scalar.
- Adding or subtracting a multiple of one row from another.
Once in the Row Echelon Form, the rank of the matrix is determined by counting the number of non-zero rows. The leading entry of each non-zero row (called the pivot) is always to the right of the leading entry of the previous row.
For example, consider the matrix:
(123000456)\begin{pmatrix} 1 & 2 & 3 \\ 0 & 0 & 0 \\ 4 & 5 & 6 \\ \end{pmatrix}104205306
In this case, there are two non-zero rows, so the rank is 2.
- Reduced Row Echelon Form (RREF)
The RREF is an extension of the REF, rank of a matrix where further simplification is done. The RREF has additional conditions where each leading entry is 1 and is the only non-zero entry in its column. To find the RREF, you continue with row operations until you achieve this form.
Once in RREF, counting the number of leading rank of a matrix ones gives you the rank. The advantage of RREF is that it provides more information about the solutions to the system of equations represented by the matrix.
- Using Determinants
For square matrices, another way to determine rank is through the use of determinants. The rank can be determined by calculating the determinants of the largest square submatrices. If a determinant of a k×kk \times kk×k submatrix is non-zero, but all determinants of larger submatrices are zero, the rank of the matrix is ok.
For example, for a 3×33 \times 33×3 matrix, if the determinant is non-zero, the rank is 3. If the largest non-zero determinant comes from a 2×22 \times 22×2 submatrix, the rank is 2.
Importance of Matrix Rank
Understanding the rank of a matrix is crucial in various fields. It serves not only as a theoretical foundation but also has practical implications in areas like statistics, machine learning, and more.
Applications in Linear Systems
One of the primary applications of matrix rank is in solving systems of linear equations. The rank helps determine the existence and uniqueness of solutions. Here’s how:
- Consistent Systems: If the rank of the coefficient matrix equals the rank of the augmented matrix, the system is consistent and has at least one solution.
- Unique Solutions: If both ranks are equal to the number of variables (columns), the system has a unique solution.
- Infinite Solutions: If the ranks are equal but less than the number of variables, the system has infinitely many solutions.
- Inconsistent Systems: If the ranks are unequal, the system has no solutions.
Signal Processing and Data Analysis
In fields like signal processing and data analysis, the rank of a matrix provides insight into the data structure. For instance, when performing Principal Component Analysis (PCA), the rank of the covariance matrix indicates the number of principal components that can be derived from the dataset.
Understanding rank helps in dimensionality reduction techniques, ensuring we retain the most significant features while discarding the less important ones.
Machine Learning and Statistics
In machine learning, matrix rank is vital in understanding model parameters and feature spaces. For example, in regression analysis, the rank of the design matrix affects the model’s ability to predict outcomes accurately. A full-rank design matrix ensures that each feature contributes uniquely to the model, while multicollinearity (highly correlated features) can lead to a reduction in rank, adversely affecting model performance.
Practical Examples of Matrix Rank
To illustrate the importance and applications of matrix rank, let’s look at some practical examples that highlight its utility in various scenarios.
Example 1: Solving Linear Equations
Consider the linear system represented by the following augmented matrix:
(123∣4246∣8369∣12)\begin{pmatrix} 1 & 2 & 3 & | & 4 \\ 2 & 4 & 6 & | & 8 \\ 3 & 6 & 9 & | & 12 \\ \end{pmatrix}123246369∣∣∣4812
Using row operations, we can transform this into a Row Echelon Form. Here, we would find that all rows are linearly dependent. Hence, the rank of the coefficient matrix is 1, while the rank of the augmented matrix is also 1. This indicates that the system has infinitely many solutions.
Example 2: Image Compression
In image processing, matrices represent pixel values. The rank of an image matrix provides insight into its complexity. For instance, if an image can be approximated with a low-rank matrix, we can compress it effectively. By using techniques like Singular Value Decomposition (SVD), we can reduce the amount of data required to represent the image while retaining essential features.
Example 3: Network Analysis
In network theory, the adjacency matrix representing connections in a network can be analyzed through its rank. A higher rank indicates a more complex network with more connections, while a lower rank might suggest redundancy or simpler structures. This analysis helps in understanding the flow of information or resources within the network.
Common Misconceptions about Matrix Rank
As with any mathematical concept, misunderstandings about matrix rank can arise. Here are a few common misconceptions clarified.
Misconception 1: Rank Only Relates to Dimensions
While the rank of a matrix is indeed related to dimensions, it also conveys information about linear independence and the relationships between rows and columns. A high rank doesn’t simply mean high dimensionality; it indicates a robust structure of independent vectors.
Misconception 2: Full Rank is Always Desirable
Although having a full rank is often beneficial, it isn’t always the goal. In cases of overfitting in machine learning models, a full-rank design matrix can lead to poor generalization. Sometimes, reducing rank through feature selection or dimensionality reduction techniques is necessary for better model performance.
Misconception 3: Rank Can Be Neglected
Some may think that rank is a secondary consideration when working with matrices. However, neglecting rank can lead to errors in calculations, especially when solving systems of equations or applying transformations. It’s crucial to consider rank in both theoretical and practical contexts.
Advanced Topics Related to Matrix Rank
As we dive deeper into the world of matrices, several advanced topics arise that are closely related to the rank of a matrix.
Singular Value Decomposition (SVD)
SVD is a powerful technique that decomposes a matrix into three other matrices, revealing its structure and rank. The singular values obtained from SVD can help in understanding the rank and essential characteristics of the original matrix.
Using SVD, we can represent a matrix AAA as A=UΣVTA = U\Sigma V^TA=UΣVT, where U and VVV are orthogonal matrices, and Σ\SigmaΣ is a diagonal matrix containing the singular values. The number of non-zero singular values indicates the rank of the matrix.
Eigenvalues and Eigenvectors
The concepts of eigenvalues and eigenvectors are closely linked to matrix rank. While eigenvalues provide insights into the scaling behavior of transformations represented by the matrix, the rank can indicate how many eigenvectors are linearly independent.
For instance, in a symmetric matrix, the number of non-zero eigenvalues corresponds to the rank, providing a deeper understanding of the matrix’s geometric properties.
Null Space and Column Space
The rank-nullity theorem is a vital concept connecting the rank of a matrix with its null space. The theorem states that for any m×nm \times nm×n matrix AAA, the following holds:
rank(A)+nullity(A)=n\text{rank}(A) + \text{nullity}(A) = rank(A)+nullity(A)=n
Here, the nullity is the dimension of the kernel (null space) of the matrix. Understanding the relationships between the rank, null space, and column space helps in fully grasping the matrix’s structure and behavior.
Conclusion
The rank of a matrix is more than just a numerical value; it encapsulates essential information about the relationships between rows and columns, plays a crucial role in solving linear systems, and has vast applications in various fields. Understanding matrix rank equips us with tools to analyze and interpret data effectively, making it a cornerstone concept in linear algebra.
In this comprehensive guide, we’ve explored what matrix rank is, how to calculate it, its significance in different domains, and addressed common misconceptions. As we continue to utilize matrices in advanced mathematics, engineering, and data science, mastering the concept of rank will undoubtedly enhance our analytical capabilities. Whether you’re an aspiring mathematician, a data scientist, or simply someone intrigued by the beauty of mathematics, the rank of a matrix is an invaluable concept to understand.